单选题
1分
一艘游轮在海上匀速航行,航向保持不变。上午8时在游轮的正东方30海里处有一灯塔。上午10时30分该灯塔位于游轮的正南方40海里处,则在该时段内,游轮与灯塔距离最短的时刻是:
参考答案: B
参考解析: 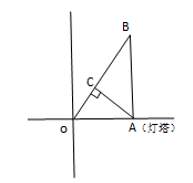
如右图所示,灯塔在A点,游轮从O点出发至B点,
OA=30海里,AB=40海里,BA⊥OA,则OB=√OA^2+AB^2=√30^2+40^2=50海里,游轮速度为50÷2.5=20海里/小时,从A点引垂线垂直OB于C点,游轮在C点位置与灯塔距离最短。
△OCA相似于△OAB,则OC/OA=OA/OB,即OC=30×30/50=18海里,游轮从O点行至C点所需时间为18÷20=0.9小时,即54分钟,故与灯塔距离最短时刻为8时54分。
故正确答案为B。